Author: Vicki Baker
School/Organization:
Philadelphia High School for Girls
Year: 2016
Seminar: The Evolving Universe
Grade Level: 9-12
Keywords: algebra, Conic Sections, ellipse, parabola
School Subject(s): Math, Science, Space
Students often wonder how school and the material they are learning relates to the real world. Math in particular, with its abstract formulas and unique vocabulary, seems obscure at best and often irrelevant to their lives. Science and math, the language of science, are two subjects with the lowest achievement indicators particularly when measured by standardized tests. Lessons with real world connections are important to improving achievement. Using astronomy with its natural science and math applications will provide an engaging, fun way to learn about the development and evolution of science in the night sky while applying them both to real life problems and mathematical content. Students, after learning the definition and calculations for conic sections will expand their knowledge of ellipses and it relates to planets
Download Unit: 16.02.03-unit.pdf
Did you try this unit in your classroom? Give us your feedback here.
This seminar, “The Evolving Universe”, examined the motion and evolution of the dynamic structures in the universe and what it our knowledge about them means for the future. The topics included observing the night sky to study the motion of the Earth, asteroids, comets, and other planets in the solar system and how they are formed, dark matter and the evolution and changing nature of other galaxies in relation to the Milky Way, our galaxy. Participants were introduced to space and the night sky so this unit will build knowledge on measurements they can do to understand the night sky, planetary movement and their relationships to conic sections. Students will be able to apply math that they learn in class to relate math to real world problems. This unit will emphasize the importance of education across both science and math as a vehicle to improve STEM knowledge using a cross curricular approach involving science and math. While it is well known today, among modern day Astronomers that the planets in our solar system move around the Sun in roughly elliptical orbits that was not always the case. Dating back to African scientists in Egypt more than 2000 years BC, buildings were aligned based on their knowledge of the sky and observations were made about the motions of the planets among the stars. Based on these observations, the ancients deduced that the planets “went around the sun”, a fact that was rediscovered by Copernicus centuries later. Exactly how the planets went around the sun, with exactly what motion, took a longer to discover” (Ridpath, 2006). In the beginning of the fifteenth century there were great debates as to whether the planets really went around the sun or not. Longstanding beliefs, linked to the church and religious principles indicated that the earth was the center of the universe. Tycho Brahe had an idea that was different from anything proposed by the ancients. Brahe believed that the debates about the nature of the motions of the planets would be best resolved if the actual positions of the planets in the sky were accurately measured. Pursuing this idea, he studied the position of planets for many years on the island of Hven, near Copenhagen. He made voluminous tables, which, after his death, were studied by Johannes Kepler, a German Mathematician (Feynman, 1995). Kepler’s work came a century after Polish astronomer Nicolaus Copernicus proposed a heliocentric theory or that the Sun lies at the center of the universe and the Earth orbits the sun, rather than the other way around. His work represented a change from the belief that the Sun and stars orbited the Earth, the center of the universe (Henderson, 2009). Kepler adopted Copernicus’ heliocentric theory but believed that the planets’ orbits were circular. Kepler tied his model of planetary motion to geometric principles. He envisioned a system in which the planets’ orbits lay within a series of nested spheres spaced according to mathematical ratios that were derived from the sizes of three-dimensional shapes that would fit within them. His model imagined a series of polygons with increasing numbers of sides that fit within the spheres. While studying the intricate tables of planets’ motions prepared by Tycho Brahe, Kepler studied the retrograde motions of Mars and fit the motions to an elliptical model (Henderson 2009). This result of this work is the Kepler’s three laws: Kepler’s first law (the Law of Orbits, 1609): Planetary orbits are elliptical with the Sun at one focus; Kepler’s second law (the Law of Equal Areas, 1618): A planet sweeps out equal areas in equal times as it orbits the Sun and Kepler’s third law (the Law of Periods, 1618): The orbital periods scale with ellipse size, such that the period squared is proportional to the semi-major axis length cubed. Kepler’s laws unified astronomy and physics and provided the foundation for expressing the behaviors on real life in terms of simple formulas (Pickover 2011). Scientists all over the world have continued to study planetary motion and achieve remarkable results. Imagine with this background and the Kepler’s laws defined in the early 1600’s the surprise in 2014 to learn that 26% of Americans believe that the sun revolves around the earth. A survey of 2,200 people in the United States conducted by the National Science Foundation (NSF) in 2012 and released in February 2014 at an annual meeting of the American Association for the Advancement of Science meeting in Chicago found that 26 percent of those surveyed answered the question “Does the Earth go around the Sun, or does the Sun go around the Earth,” incorrectly. In the same survey, just 39 percent answered correctly (true) that “The universe began with a huge explosion” and only 48 percent said “Human beings, as we know them today, developed from earlier species of animals.” (NSF, 2014) While an interesting discussion could be had concerning the forces and circumstances driving these results, more exposure to the subject matter in ways that help students retain the knowledge seem warranted. Current educational pedagogy includes strategies to increase student learning called “Authentic learning” The Journal of Authentic Learning defines authentic learning as learning through applying knowledge in real-life contexts and situations. In the article the author, Audrey Rule, indicates that authentic learning isn’t an instructional model as much as it includes four themes: Rather than learning facts and figures this approach allows students to feel they are part of the work and the outcomes can be relevant to their lives. This unit will use the authentic learning approach in the three lessons combining conic sections and astronomy.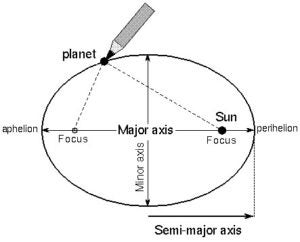
2. Use of open-ended inquiry, thinking skills and metacognition.
3. Students engage in discourse and social learning in a community of learners.
4. Students direct their own learning in project work.
This unit is designed to connect high school course content in math and science to real world happenings using the night sky. Specifically, the unit is for high school mathematics students enrolled in a math course meeting five days per week for fifty-five minute periods. The objectives of the unit will include the following:
This curriculum unit will meet the objectives discussed above through hands-on and problem based conic section lessons related, in the end to astronomy. The Pennsylvania Common Core Standards for both mathematics and science will be addressed by students identifying conic sections and modeling then from real-life examples, deriving and interpreting equations and using new concepts to apply conic section knowledge to astronomy.
Lesson 1: Finding Equations Using Real Life Images This lesson is a follow-up lesson after students have a thorough understanding of parabolas: equations (standard form and factored form), finding the vertex, finding the coordinates of the axis of symmetry, solutions). Lesson can be modified to find equations for ellipses and hyperbolas in future lessons. Pre-work: Student pre-assignment. Select a picture which has a parabolic shape from a magazine, newspaper or from the internet (example satellite dish, firework, path of ball, diver). Lesson Objective: Students will gain an appreciation for real life conic sections by creating parabolic models of parabolic shapes found in normal life circumstances. Students will demonstrate their knowledge of conic sections by solving the equation that their picture, superimposed on graph paper crates. Materials: (Example: 36 x 5 Yard Vellum Roll, 10×10 Grid – Amazon.com) Procedure: Lesson 2: Hands-on Ellipse with a String (adapted from Holt Algebra 2 p. 586 ©2003) This lesson provides a hands-on activity where students will discover the parts of an ellipse by creating one from a few tools. They will understand the parts of an ellipse and the relationships of the parts to the subsequent equation. Materials: Blank sheets of graph paper (3 sheets) Cardboard 2 tacks Ruler (cm) 3x long piece of string (1×20 cm,2 other lengths 1 larger 1 smaller) Pencil or marker Procedure: (Read all the directions prior to beginning the lesson) Part 2 Mars orbits the sun in an elliptical path whose minimum distance from the Sun is 129.5 million milers and whose maximum distance from the Sun is 154.4 million miles. The Sun represents one focus of the ellipse. Write a standard equation for the elliptical orbit of Mars around the Sun, where the center of the ellipse is at the origin. 4.Find b2 Analysis: Answer these questions in complete sentences on a separate sheet. Lesson 3 The eccentricity, (E), of an ellipse, the measure of how round or flat its shape, is the ratio of the distance, c, between the center and a focus to the distance, a, between the center and vertex.
Ellipse #
Focal Distance (cm)
Major Axis (cm)
1
2
3
Planet
Eccentricity
Mercury
0.206
Venus
0.007
Earth
0.017
Mars
0.093
Pluto
0.048
Jupiter
0.056
Saturn
0.047
Uranus
0.008
Neptune
0.247
Ellipse #
Focal Distance (cm)
Major Axis (cm)
Eccentricity
1
2
3
4
Works Cited The Components of Authentic Learning” by Audrey Rule, Journal of Authentic Learning Volume 3, Number 1, August 2006, Pp. 1-10. Journal article providing as quick synopsis of authentic learning. Good summary of using real-world problems, inquiry and thinking skills, discourse in a community of learners, student-directed learning. Feynman, Richard P., Robert B. Leighton, and Matthew L. Sands. Six Easy Pieces: Essentials of Physics, Explained by Its Most Brilliant Teacher. Reading, MA: Addison-Wesley, 1995. Print. This is non-technical physics primer based on the knowledge of scientist Richard Feynman’s book The Feynman Lectures on Physics. Topics are described in qualitative terms with some formulas were needed. Henderson, Mark, Joanne Baker, and A. J. Crilly. 100 Most Important Science Ideas: Key Concepts in Genetics, Physics and Mathematics. Buffalo, NY: Firefly, 2009. Print. The science ideas presented here represent key science and physics topics. The short descriptions are valuable in their simplicity. Pickover, Clifford A. The Physics Book: From the Big Bang to Quantum Resurrection, 250 Milestones in the History of Physics. New York: Sterling Pub., 2011. Print. Beautifully illustrated, this book of milestones provides quick, informative information on major physics principles. Ridpath, Ian. Astronomy. London: Dorling Kindersley, 2006. Print. An overview of Astronomy. This book contains information on the history of astronomy, the theories of the universe (origins, solar system, stars) and information for observations in the night sky. The zodiac maps allow the reader to expand from constellations to answer “what’s your sign”. “Science and Engineering Indicators 2014.” Nsf.gov. N.p., n.d. Web. 14 February. 2014. This article summarizes the finding of a NSF study of scientific knowledge. National Council of Teachers of Mathematics, n.d. Web. 02 Aug. 2016. An organization dedicated to mathematics education, this website and its Illuminations section provide authentic lessons of many types. Darling, David. “Ellipse.” Ellipse. N.p., n.d. Web. 13 Aug. 2016. Narrative, formulas and diagrams for ellipses Resources Teacher Resources Daniels, Patricia. The New Solar System: Ice Worlds, Moons, and Planets Redefined. Washington, D.C.: National Geographic Society, 2009. Print. The New Solar System shows provides background and imagery with awe inspiring pictures from satellites and spacecraft to remarkable close-ups of planets. Complete glossary of terms and web addresses make this a valuable resource. Annotated Teachers Edition Algebra 2 Schultz Ellis Hollowell Engelbrecht Holt Rinehart Winston 2003 This textbook includes lesson on conic section which include astronomy. Raymo, Chet. An Intimate Look at the Night Sky. New York: Walker, 2001. Print. An informative book for the astronomy enthusiast provides pictures and information on the night sky. Containing 24 star maps, information on what the naked eye can see in the night sky allows the reader the gain knowledge for the sky without sophisticated equipment. The Retrograde Motion of Mars. Erlichson, Herman, Physics Teacher, v37 n6 p342 Sep 1999 Retrograde motion is key to understanding planet orbits and the part it plays in astronomy. “Retrograde Motion of Mars « Free Lessons | Teacher Created Resources.” Retrograde Motion of Mars « Free Lessons | Teacher Created Resources. N.p., n.d. Web. 13 Aug. 2016. “Comic Section Explorer.” National Council of Teachers of Mathematics, n.d. Web 8 Aug. 2016. (Styrofoam materials for conic sections can be purchased from a crafts store such as Jo Ann Fabrics) This site guides students though an exercise to discover conic sections by cutting Styrofoam cones with planes at different angles. The results are each of the conic sections: Circle, parabola, ellipse, hyperbola. “Dynamic moving model.” National Council of Teachers of Mathematics, n.d. Web. 13 Aug. 2016. This site provides a dynamic model that allows students to move a conic section in a plane and change the angle and points on the cone. The resulting changes in the cone help to reinforce the transformation that are possible using conic sections. Elliptical Orbits. J. Robert Buchanan, n.d. Web. http://banach.millersville.edu/~bob/math160/Ellipses/main.pdf Planetary orbits and particularly elliptical orbits are discussed. Student Resources “Astronomy Resources.” Student Guide Astronomy Resources Comments. N.p., n.d. Web. 13 Aug. 2016. This book contains significant information for the study of astronomy.
CC.2.1.HS.F.4 Use units as a way to understand problems and to guide the solution of multi-step problems. CC.2.2.8.B.3 Analyze and solve equations CC.2.2.8.C.1 Define, evaluate, and compare functions. CC.2.2.8.C.2 Use concepts of functions to model relationships between quantities. CC.2.2.HS.C.3 Write functions or sequences that model relationships between two quantities. CC.2.2.HS.D.7 Create and graph equations …to describe numbers or relationships. Graph and analyze functions and use their properties to make connections between the different representations. CC.2.2.HS.C.3 Write functions or sequences that model relationships between two quantities. Graph and analyze functions and use their properties to make connections between the different representations. CC.2.2.HS.C.3 Write functions or sequences that model relationships between two quantities. CC.2.2.HS.C.5 Construct and compare linear, quadratic, and exponential models to solve problems. CC.2.2.HS.C.6 Interpret functions in terms of the situations they model. CC.2.4.HS.B.1 Summarize, represent, and interpret data on a single count or measurement variable. Science
Anchor Descriptor
Core Standard
A1.1.2.1 Write, solve and /or graph equations using various methods
CC.2.1.HS.F3Apply quantitative reasoning to choose and interpret units and scales in formulas, graphs and data displays
A1.2.1.1 Analyze and/or use patterns or relations.
CC.2.2.HS.C.2
A1.2.2.1 Describe, compute, and/or use models to describe functions
CC.2.2.HS.C.2
Anchor Descriptor
Core Standard
Science & Technology
Conduct multiple step experiments
Apply appropriate tools, materials and processes to solve complex problems