Author: Bridget Mason
School/Organization:
The Academy at Palumbo
Year: 2017
Seminar: Is There Any Life in the Worlds Beyond Our Own?
Grade Level: 9
Keywords: astronomy, combination, compound probability, counting principle, dependent events, experimental Probability, habitable planets, habitable zone, independent events, multiplication, mutually exclusive events, overlapping events, permutation, probability, sample space, Theoretical probability
School Subject(s): Algebra, Math
Basic high school Algebra is often taught in relative abstraction from topics relevant to students’ lives, but has the potential to be very concrete and, as a result, more engaging for all students. Probability is a concept often left for the end of the year and taught with very little cohesion to the rest of the topics in Algebra. Additionally, the examples provided in textbooks are often low-level and can lack relevance for students. This unit however, would allow students to use their own personal experiences in their own specific circumstances in conjunction with a new grasp on probabilistic thinking in order to gain a more meaningful understanding of probability in the context of the universe.
This unit is designed for my 9th grade Advanced Algebra classes, which meet five times per week for 48 minutes per day, to complete in around two and a half weeks. Students are expected to have completed most of Algebra 1 by the time they reach this unit and should have a strong grasp on arithmetic and the ability to reasonably argue whether or not a determined solution makes sense in the context of a given question or problem. Prior knowledge of astronomy or compound probability is not required, but students should have a firm grasp on how to convert between fractions, decimals, and percents.
Download Unit: Mason-B-Unit.pdf
Did you try this unit in your classroom? Give us your feedback here.
Algebra is one of the first math classes in which students have the opportunity to ask and answer the question, “Does this make sense?” Particularly when applying algebra to analyze and draw conclusions about the world around them, students can use their lifetime of prior experience to determine if an outcome could possibly “make sense” for a given situation. When students synthesize given information, determine the relevant details necessary to answer a specific question about the information, and perform appropriate operations to calculate a meaningful answer to a question, they can more deeply learn and understand concepts that can often seem abstract and immaterial. Probability is a topic within high school-level math for which the application of the question “Does this make sense?” is especially relevant. Students must recognize that the likelihood of a given event is predicated on specific circumstances, that slight variations in those circumstances can drastically change the likelihood of that given event, and that outcomes in experimentation may differ from those predicted in theory even if calculations were correct and logic was sound. The goal of this unit is to empower students to learn about and use the universe as a means by which to extend their understanding of basic probability to answer questions like: Are we alone in the universe? What is the probability that there is another planet capable of hosting intelligent life? Students will use these skills to make meaningful predictions and estimations about the likelihood of given events in the universe rather than blindly applying algorithms. In order to support students in their effort to determine answers to these complex questions, this unit will provide a scaffolded sequence of lessons and activities designed to lead students from a basic understanding of probability to one that they can apply broadly and flexibly in variable and unfamiliar situations. The lessons in this unit will guide students of varying mathematical abilities and diverse socioeconomic backgrounds in building an understanding of the probability they already practice in their daily lives to a stronger comprehension of how these same ideas can be applied to a vast array of contexts, including one so overwhelming and seemingly impossible as determining the probability of the existence of other life in our universe.
The Algebra Project’s mission states, “every child has a right to a quality education to succeed in this technology-based society and to exercise full citizenship.” (Moses, Cobb) With the Doomsday Clock at 2.5 minutes to midnight (Bulletin of the Atomic Scientists) and recent cuts to the federal budget for research and work in environmental and space sectors, extra-planetary consideration and exploration is not only interesting, but of critical importance for all of humanity. The more students who are exposed to and interested in this topic, the better the chance that human civilization has to preserve itself. These concepts are more complex and higher level than those typically taught in a high school Algebra course, but there is plenty of easily relatable and digestible content on which students will build an understanding. A student uses probability, often without realizing it, throughout their day: they estimate the probability of getting caught using cell phone in class, that they’ll be assigned homework over a weekend or break, that the vending machine will be out of water bottles on a hot day. This unit is designed to make students more conscious of those situations and the thinking they use to make predictions or estimates. They will use this greater awareness of their own decision-making processes and greater understanding of probabilistic reasoning to make logical decisions about situations, and extend that understanding of probability to situations beyond their own experiences. Basic high school Algebra is often taught in relative abstraction from topics relevant to students’ lives, but has the potential to be very concrete and, as a result, more engaging for all students. Probability is a concept often left for the end of the year and taught with very little cohesion to the rest of the topics in Algebra. Additionally, the examples provided in textbooks are often low-level and can lack relevance for students. This unit however, would allow students to use their own personal experiences in their own specific circumstances in conjunction with a new grasp on probabilistic thinking in order to gain a more meaningful understanding of probability in the context of the universe. Because student engagement is a primary motivation for this unit, my goal will not only be for students to understand the identified content, but also to provide opportunities for practice through gamification both of my own creation and of students’ creation. Additionally, my students love to debate, but often struggle to use evidence to back their arguments. In the process of working through progressively more complex applications of probability, I want my students to become accustomed to justifying the calculations that they perform and identifying faulty logic when math “doesn’t make sense” in a specific context. The unit is initially designed for my 9th grade Advanced Algebra classes, which meet five times per week for 48 minutes per day, to complete in around two and a half weeks. Students are expected to have completed most of Algebra 1 by the time they reach this unit and should have a strong grasp on arithmetic and the ability to reasonably argue whether or not a determined solution makes sense in the context of a given question or problem. My students are very diverse, have wildly different mathematical abilities and interests, and will likely have had no experience applying probability calculations to what they know about the universe. I will assume that most of my students have very little knowledge about the universe, terrestrial planets, and the probability of life beyond our own. I will also assume that most students have had some very basic exposure to concepts of probability, but that they will all need a thorough review, if not an outright introduction, before they are able to apply these concepts in a more complex context. Like most high school students in Philadelphia, my students are required to take and pass the Keystone Algebra 1 Exam in order to graduate. Inevitably, much of the content and delivery of material in my class hinges on that requirement. Because of the breadth of material covered on the exam and the level at which most students enter my Algebra 1 class, preparation for this test feels of greatest importance. Though I often make room for shorter projects and always try to provide examples of mathematical concepts in meaningful and relevant contexts, this unit is unique in the exploration it allows and encourages, particularly in the application of probability in a relevant but largely unfamiliar context. By design, there will be more time for inquiry and argumentation than in other units. My hope is that this time and the resulting questions, discussions, and understandings will be a catalyst in sparking students’ further interest in higher level math and all of its possible applications.
The intent of the chosen objectives is to provide a strong foundational understanding of basic probability in order that students apply that understanding to increasingly complex questions about intelligent life on planets other than our own. Students will consider sample spaces and be able to explain when order does and does not matter. They will grapple with the ideas of experimental and theoretical probability, how the two are related, and how they are distinct. After developing a stronger grasp on these topics, students will consider what predictions they can make when they are determining the likelihood of multiple related or unrelated events. The mastery of all of these objectives will culminate in students using their understanding of various aspects of probability to produce logical responses to questions about our universe and the possibility of intelligent life beyond our own. The objectives of the unit will include:
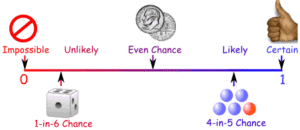
Often my students know very little about the world around them, let alone the universe beyond this planet. I want to expand students’ awareness of the size of our galaxy, the size of the universe, and how they can most accurately attempt imagine themselves in the context of the vastness of both of the above spaces. The goal is that they come away from this unit both with a firm grasp on probability and an understanding of how (im)probable it is that our planet exists with us on it, as well as how probable it is that there is other intelligent life somewhere in the universe. My goal is to challenge students to realistically imagine life beyond our own via a deeper grasp of probability and a more comprehensive understanding of our planet in the universe. I want to hook students with the Drake Equation, explaining and substituting the values below. where If we substitute, N 10 technological civilizations in just the Milky Way Galaxy (NASA Goddard Space Flight Center) I want my classes to consider what might be required for the existence of intelligent life, so we will spend some time discussing what it means to be an “earth-like” planet and what kind of communication would be necessary for us to discover a planet like this. We’ll start with a basic discussion of Earth’s probability; all of the factors that were required for our civilization to exist as we know it, and the likelihood that everything happened so that the human species exists in its current form on planet Earth. I will then scale back the complexity of the probability in question and approach the topic from a more student-friendly level with hands-on activities, immediately relevant context, and more manageable calculations that students are able to accurately apply and perform with ease. I want students to begin to recognize the frequency with which the use (effectively or not) the idea of probability in the moment-to-moment decisions they make every day. We will start each new objective with a calculation that every student is capable of performing without any knowledge of formulas or prior experience with probability. With this goal in mind, each lesson will be designed to be accessible to every student, regardless of ability. Additionally, there will be possible extensions of each lesson for those students who grasp the material with ease. Nearly all of my students are accustomed to calculating an answer in a context where there is a single correct answer, and the vast majority of them stop at whatever value they calculated without looking for error or asking if the answer is logical within the given context. My challenge is going to be to help them both establish a degree of comfort working with mistakes, and to become more comfortable with the uncertainty involved in calculating probabilities for hypothetical situations about which we may not have complete information. I want them to constantly be asking of themselves and of each other if their calculations could possibly make sense and, even if those calculations “make sense” what unpredicted variants might affect the accuracy and legitimacy of their calculations. Throughout the school year, regardless of the content, my students check their own work, check each other’s work, and argue as a class about whether or not an answer is correct and why. This unit will require students to continue that practice with the added challenge of a very complex context. In each lesson, I will ask students to consider the situational variability and how minimally or drastically it will change the probability of a specific outcome. Students will discuss within small groups why and how changing any part of an event affects the possible outcomes. Research debates whether probability is intuitive or counterintuitive for students. I will focus on clarifying both the reasoning behind the mathematical processes we use to reach conclusions about the probability of an event(s) and why the conclusions we reach make sense in their contexts. For example: Why isn’t the probability of flipping two heads ½ instead of ¼? Is that intuitive or counterintuitive? Is this reaction the same for all students? I plan to explain mathematical concepts parallel to experiments and the creation of sample spaces to help students see the relatedness. Common student misconceptions and accompanying teaching strategies: Teaching strategy: clarify simple vs compound events, discuss equiprobability in context and provide examples and non-examples. (Koellner, Pittman and Brendefur) Teaching strategy: Ask if one trial provides enough information for you to make a decision (which is easy to prove false when two or more groups of students have determined different experimental probabilities for same events). Ask students how many trials should we conduct in order to have a large enough sample size for an accurate estimation and discuss the differences and relatedness of the concepts of theoretical and experimental probability. (Koellner, Pittman and Brendefur)![]()
Objective(s): SWBAT identify and analyze various circumstances in which they use probabilistic thinking in their daily lives SWBAT learn about the background and application of the Drake Equation in order to begin imagining the probability of intelligent life beyond our own Trivia/Background: How many planets are there in our universe? Materials: Drake Equation Animation https://www.youtube.com/watch?v=80Ryq6bH2aY (da Silva and Dudnik) Activity: This lesson will be primarily focused on inspiring students to think critically, ask questions, and strategize methods of determining answers to those questions. I will begin class by introducing the idea of variability and asking students “What do you have to consider if you want to get to school on time?” I anticipate that they’ll come up with answers about setting alarms, having to share a bathroom with family members, catching busses, traffic, lines at Dunkin Donuts, etc. Once we’ve determined a substantial list of variables that affect getting to school on time, I’ll ask them about the likelihood of getting to school on time if certain variables are fixed or if other variables are added. After we’ve discussed and analyzed this first example, I’ll ask groups to come up with at least three other examples of using probabilistic thinking throughout their days. If groups are struggling in this discussion, I’ll prompt them with other examples of times in the day when they might unconsciously or consciously use probability to make a decision. Groups will share their ideas with the class, clarify any misunderstandings, and debate any disagreements. When all groups have shared their thinking, I’ll ask the class what they think the likelihood is that ours is the only planet on which inhabitants are thinking, about probability or anything else. When students begin to answer, I’ll ask them for justifications for their answers and allow students to question or challenge each other’s answers. After a brief discussion of this question, we will watch the animated short video about the Drake Equation. Students will be instructed to write down at least two things they think we need to know in order to find other intelligent life in our universe. We will conclude the class with a brief discussion of the knowledge requirements that students noted during the video. Their homework will be to write three or more sentences about what they think intelligent life on another planet might look like and require. Assessment: I will conduct an informal assessment during discussions to ensure that students have at least a general idea that probability has to do with the likelihood of an event given the variables. Objective(s): SWBAT use the multiplication counting principle, find permutations, and use permutation notation Trivia/Background: What makes a planet habitable or “earth-like”? Materials: Permutation prompts, permutation notation, visual of “habitable zone” Activity: The discussion for today will continue where we left off yesterday. I will ask students to share their writing about the possibility of intelligent life on other planets. We will categorize answers as either “planetary requirements for intelligent life” or “characteristics of extraterrestrial intelligent life.” Once the class has exhausted their responses, we will examine a diagram illustrating what a “habitable zone” is and discuss the requirements for a planet to be considered habitable. I will ask students about what they think can exist in the habitable zone (liquid water!) and why (not too hot to evaporate the water, not too cold to freeze it). We will briefly discuss other basic requirements and why scientists assume those requirements, including a sun-like star, a rocky make-up, and an earth-like size and orbit. There are countless requirements for a planet to be able to support life and we would need to consider a vast array of composites of those requirements in order to imagine all possible earth-like planets. To make this concept significantly more manageable, we’ll start on a much smaller scale – choosing class officers. In small groups, students will work to answer and explain the following questions: I will give groups sufficient time to think about and determine answers to those three questions. Each group will write down their three answers and submit those answers at the end of time (so that I don’t have one group answer first and every following group change their answers to match the first group). I’ll record the submissions on the board and the class will discuss which submissions they thought were correct and why. After this discussion, I’ll ask the class to quickly tell me how many different ways we could choose a President, Vice President, and Secretary from all 32 (give or take a few) students in the room. If a student or students have a quick method for determining this answer, I’ll ask them to explain their reasoning to the class. We will then discuss the use of permutation notation for situations in which the possible permutations are so large that diagramming and listing becomes more tedious and time-consuming than is feasible within the confines of a class period: The expression nPr represents the number of permutations of n objects arranged r at a time. nPr = n!/((n-r)!) Example 8P2 = 8!/((8-2)!)=8!/6!=(8∙7∙6∙5∙4∙3∙2∙1)/(6∙5∙4∙3∙2∙1)=56 We will use permutation notation to determine the different possible groups of students that could fill the student council positions as a class. I will then provide students with three or more practice problems (dependent on time) to complete in their small groups. When there are five minutes remaining in class, I will ask student volunteers to post their answers and address any questions from their classmates. Objective(s): SWBAT use the multiplication counting principle, find combinations, and use combination notation Materials: Combination prompts, combination notation, Activity: I’ll ask students to remember the prompts that we worked on yesterday with permutations. Our principal had three free general admission tickets to Beyonce’s show. If she’s choosing from the five students with the best grades in the freshmen class, how many different groups of students could she pick? (I anticipate that many students will attempt to use permutation notation and will circulate around the room to highlight any students that push back or to prod groups to recognize how this question is different from all of the ones we addressed yesterday). If and when groups come up with an answer, I’ll ask them to organize their lists of groups. When at least a few groups have successfully recognized that they cannot use the same calculations they used yesterday for this situation, we’ll discuss as a class how the prompt today was different than the prompt yesterday. In the discussion, students should be able to conclude that order was a factor in the prompt provided yesterday (about student council positions) and that order was not a factor in the prompt provided today. I will ask students for suggestions to best organize the information to determine all of the possible combinations for which order isn’t a factor and I will purposefully include repeat combinations in a different order to elicit student opposition and an explanation for why the repeated combination shouldn’t be counted in our total. After any student questions have been answers and misunderstandings addressed, I’ll ask students how their answer would change if our principal were choosing a group of three students from the entire freshman class, which contains approximately 230 students. I predict that few, if any, students will immediately be able to determine this answer. If any student is able to quickly determine the answer, I’ll ask the student to explain their reasoning, and then introduce combination notation, which similar to permutation notation, is particularly useful when diagrams and lists are not time or effort effective for given prompts: The expression nCr represents the number of combinations of n objects arranged r at a time. nCr = n!/(r!(n-r)!) Example 8P2 = 8!/(2!(8-2)!)=8!/2!6!=(8∙7∙6∙5∙4∙3∙2∙1)/((2∙1)(6∙5∙4∙3∙2∙1))=28 After this discussion, I’ll give groups the below list of situations and ask them to determine if the situations represent a permutation or a combination, and then calculate the total number of options. Individuals will provide their answers and a brief justification and other students will be given the opportunity to either agree with the given answer or disagree and provide a different justification. Assessment: For homework, I will ask students to craft four situations, two of which are permutations and two of which are combinations. I will ask them to write at least one sentence for each situation explaining which it is either a permutation or a combination. Objective(s): SWBAT define, differentiate, and find theoretical and experimental probabilities Materials: Coins for experimental probability activity Activity: To start class, I’ll ask students which game show they would rather be a contestant on: Option 1: You win $10,000 if you spin the wheel pictured (wheel with 12 spaces, two of which are red) and land on either of the red spaces. Option 2: There is a prize behind one of five doors. You win $5,000 if you choose the right door. Neither option is objectively correct, so the goal is to get students discussing the value of risk and begin to associate that risk and chance-taking with probability. (Pierce) I will ask students to give a succinct definition of probability – most (if not all) have defined and used the term in a prior academic context and will be able to relate it to the likelihood of an event. I will project the above visual of probability on a scale from 0 to 1 and ask students to give a few examples and explain where and why they think those examples fall on the spectrum of probability. We can find the probability of an event either by reasoning mathematically or performing experiments and collecting data In theory probability is the fraction of favorable outcomes (the outcomes we want) out of the total number of possible outcomes. We say “in theory” because we are reasoning mathematically and these events haven’t actually taken place. The theoretical probability of an event is found by using the formula below: P(event) = (number of favorable outcomes)/(total number of possible outcomes) where the probability of an event can be expressed as a fraction, a decimal, or a percent. In the Milky Way galaxy (our galaxy!), there are approximately 100 billion planets and of those 100 billion, 40 billion are “earth like.” (Overbye) What is the theoretical probability that a planet selected at random is “earth like?” The complement of an event is the probability that the event will not occur. So if we were to ask the same question above but want to know what the theoretical probability is that a planet selected at random is not earth like, we can use the formula P(not event) = 1 – P(event). I will ask students if in this first problem we were using mathematical reasoning or if we were collecting data (hopefully this will be obvious). Theory sometimes doesn’t entirely match the outcome for every experiment we perform of an event. I’ll ask each group to flip a coin 10 times and record the outcomes. Most groups will not find an outcome of exactly five heads and five tails. However, if we combine the results of all the groups, the experimental probability will likely begin approaching a 50% likelihood of flipping a heads. If repeated, the experimental probability of an event should be increasingly close to the theoretical probability of that same event. Using data taken from the School District of Philadelphia’s website about the Academy at Palumbo’s student population (The School District of Philadelphia), students will answer the following questions and give answers as a fraction, decimal, and percent: Students will work in groups to determine these answers and we will discuss the answers prior to the end of class. I anticipate some student confusion for questions 3, 4, and 5, so I will ask students with the correct answer to those questions to prepare explanations for their classmates. Objective(s): SWBAT find probabilities of mutually exclusive and overlapping events Trivia/Background: If we were to scale down the entire history of the universe to a single year, approximately how long do you think a human life would last? Approximately how long do you think humans have been around? (Answer: .23 seconds for the length of a human life, about 3 hours for the existence of the species After students take guesses, I will project the cosmic calendar found at http://www.cosmiccalendar.net/) (Fisk) Materials: dice, coins, decks of cards Activity: Each group will have two decks of cards at their tables. I will ask them to find the following two probabilities. Once the groups have come up with their answers, I’ll ask students to share the probabilities they found and explain their reasoning. I will also ask how the two questions were different (other than that they asked students about different cards). Once a student or students mention that there was an overlap in the second group of cards (there is one queen that is also a heart), I will introduce the terms mutually exclusive and overlapping to describe the two different prompts. If there are no overlapping items, then P(A or B) = P(A) + P(B) If there are overlapping items, then P(A or B) = P(A) + P(B) – P(A and B) In groups, I will have students find the probability of After discussing student results, clarifying any misunderstandings, and answering any questions about the above prompts, I’ll ask students to consider all the possible outcomes if we flip a coin twice. They should come up with a sample space of four outcomes (HH, HT, TH, TT). I’ll ask them what the probability is of flipping two tails (¼ or 25%) and then ask them to think about the math behind that number. I’ll then ask students to try to determine the probability of flipping a coin four times and getting four tails. Some groups will likely struggle and I’ll bring them back to the first problem and ask them to think about where that ¼ came from and how they can use that information to calculate the probability of four tails. After groups have all reached the conclusion that the probability of flipping four tails is 1/16 or 6.25%, I’ll introduce the term compound probability as the likelihood of two or more independent events. If A and B are independent events, then P(A) * P(B) = P(A and B) To clarify the term independent I’ll give students the following scenarios and ask them to decide in which does the first event change the outcome of the second. These examples should be fairly obvious to students and should help illustrate the difference between independent and dependent events. Assessment: For homework, I’ll ask students to come up with two examples of dependent events and two examples of independent events and write a sentence explaining why each set of events is either dependent or independent. Objective(s): SWBAT find probabilities of independent and dependent events Trivia/Background: Short video about Kepler Telescope and newly discovered earth like planets (from June, 20017) https://www.youtube.com/watch?v=qBMuRxJqaR0 (Al Jazeera English) Materials: dice, coins, deck of cards, video questions Activity: I will ask students to consider the following situation and why the work provided is incorrect and how it should be changed in order to calculate a correct answer. There are 14 male teachers and 26 female teachers at Palumbo. Two teachers are chosen for an award. What is the probability that both teachers are female? Work: (26/40)*(26/40)=676/1600 reduces to (169/400)= 42.25% Students should recognize that the first teacher chosen cannot be chosen twice, so that would reduce the number of available female teachers in the numerator of the second fraction to 25. Students should also recognize that once the first teacher is chosen, the pool of available teachers from which to choose for the second award shrinks to 39. Groups of students should determine the correct work as found below: Work: (26/40)*(25/39)=650/1560 reduces to 5/12=41.67% In determining appropriate calculations, students will have to ask themselves if the pools of favorable outcomes and total outcomes have changed (and how they’ve changed) after the first event. If A and B are dependent events, then P(A) * P(B after A) = P(A then B) In groups, students will use their cards (for some examples) to determine if the following situations depict independent or dependent events and then to calculate the probability of those compound events. Students will watch the short film about the Kepler Telescope and newly discovered planets. While watching, they’ll jot down the follow figures to answer some compound probability questions: 4035 likely planets, 50 earth like planets, about 2000 planets that were gaseous/frozen/boiling. In theorizing the probability of discovering these earth like planets based on Kepler data, what else might we want to consider? (earth like planets are often much smaller and may be harder to detect, so that probabilities we calculated are probably much larger than the actual probability of Kepler detecting those planets!) Day 7 – 9: Students will complete a slight adaptation of the “Design Your Own Game” Project, originally from the blog “I Want to Teach Forever.” The adaptation of the game can be found in the appendix. (DeRosa) Day 10: Students will take a short formal assessment based on past standardized test problems and including constructed response prompts to demonstrate their understanding of probability.Day 1: How do we use probability every day? What is the probability that we are alone in the universe?
Day 2-3: Permutations and Combinations – Decisions, Decisions, Decisions
Day 2
Day 3
Permutation or Combination?
Day 4: Theory versus Practice
Black
419
White
113
Asian
242
Latino
84
Pacific Islander
0
American Indian
4
Other
46
Day 5-6: Compound Events
Day 5
For two events A and B
For two events A and B
Day 6
For two events A and B
Day 7-10: Project – Planetary Probability
Planetary Probability: Design Your Own Game In this assignment, you will be designing your own game in groups. The game should be the type of game that you would play at a carnival, amusement park or at home with your friends. It cannot be a game that already exists— your group must create a unique game. You must be able to explain the probability of your game, so don’t make it too complicated! LASTLY, your game must be universe-themed and should include at least ONE thing your group has learned about in our discussion about the search for intelligent life beyond our own! Final Products: Grading: See rubric (next page). The Write-Up What were your overall feelings about this project? Did this project help you understand the probability any better? How did your group work together (be sure to include your groupmates names) Were there any group members that didn’t pull their weight? Any group members who tried to boss the group around? What do you think about the probability of discovering intelligent life on other planets. RUBRIC Appendix: Probability Project
CATEGORY
4
3
2
1
Game
Students create a fully functioning game that students can play. They bring all of the game materials to class.
Students create a game that students can play. There may be slight over-sights, but overall the game can be played.
Students create a game, but it cannot be played in class.
Students have an idea for a game.
Instructions
Instructions are clear and easy to follow. The game can be played by others without referring to the game creators for help.
Instructions are somewhat clear and easy to follow. The game can be played by others with minimal interaction with creators of the game.
Group has written instructions but they are unclear and a verbal description of the game is necessary.
Instructions are incomplete.
Group Write-Up
Group has comprehensive write-up including: introduction, instructions, game description and probability analysis. The write-up has been thoughtfully prepared and provides insight into the actions of the group.
Group has write-up including: introduction, instructions, game description and probability analysis. The write-up provides some insight into the actions of the group.
Group has an incomplete write-up including some of the following: introduction, instructions, game description and probability analysis.
An attempt at a write-up is made.
Probability Analysis
Group provides accurate analysis of the math behind their game. The idea of a fair game is clearly explained in terms of their project and an alternative for making their game fair is presented.
Group provides somewhat accurate analysis of the math behind their game. The idea of a fair game is explained in terms of their project. An attempt at providing an alternative for making their game fair is presented.
Group provides some analysis of the math behind their game. The idea of fair game is mentioned.
Group attempts some sort of analysis of their probability.
Individual Reflection
Reflection clearly explains students thought process during the project. The student’s thoughts about the probability of life in the universe are clearly described.
Reflection attempts to explain students thought process during the project. The student’s thoughts about the probability of life in the universe are described.
Reflection attempts to explain students thought process during the project.
Some attempt at a reflection is made.
Neatness and Organization
The work is presented in a neat, clear, organized fashion that is easy to read.
The work is presented in a neat and organized fashion that is usually easy to read.
The work is presented in an organized fashion but may be hard to read at times.
The work appears sloppy and unorganized. It is hard to know what information goes together.
Ahlgren, Andrew and Joan Garfield. “Difficulties in Learning Basic Concepts in Probability and Statistics: Implications for Research.” Journal for Research in Mathematics Education (1988): 44-63. Al Jazeera English. NASA’s Kepler Space Telescope Finds 10 Earth-Like Planets. 19 June 2017. 20 June 2017. <https://www.youtube.com/watch?v=qBMuRxJqaR0>. Brennan, Pat. NASA. n.d. 12 June 2017. <https://exoplanets.nasa.gov/the-search-for-life/habitable-zones/ >. Bulletin of the Atomic Scientists. Doomsday Timeline. 26 January 2017. 11 April 2017. <http://thebulletin.org/timeline>. Charles, Randall, et al. “Data Analysis and Probability.” Charles, Randall, et al. Algebra 1: Common Core. Boston: Pearson Education, 2015. 723-791. da Silva, Wilson and Andrzej Dudnik. Drake Equation. 9 August 2013. Video. 12 June 2017. <https://www.youtube.com/watch?v=80Ryq6bH2aY>. DeRosa, Tom. Design Your Own Carnival Game activity. 26 April 2016. 14 April 2017. Fisk, Eric. Cosmic Calendar. 15 February 2012. 14 April 2017. <http://www.cosmiccalendar.net/>. Hawking, Stephen. Life in the Universe. n.d. 10 4 2017. <http://www.hawking.org.uk/life-in-the-universe.html>. Koellner, Karen, Mary Pittman and Jonathan Brendefur. “Expect the Unexpected When Teaching Probability .” Mathematics Teaching (2015): 29-32. Konold, C. “Understanding Students’ Beliefs About Probability.” Glasersfeld, E. Von. Radical Constructivism in Mathematics Education . Dordrecht: Kluwer, 1991. 139-156. LeCoutre, V.P. “Cognitive Models and Problem Spaces in “Purely Random” situations.” Educational Studies in Mathematics (1992): 557-568. NASA Goddard Space Flight Center. Imagine the Universe! Lotto or Life: What Are the Chances? . 8 3 2017. 12 6 2017. <https://imagine.gsfc.nasa.gov/educators/lessons/removed/lotto/lotto.html>. Overbye, Dennis. “Far-Off Planets Like Earth Dot the Galaxy.” 4 November 2013. The New York Times Space and Cosmos. 12 June 2017. <http://www.nytimes.com/2013/11/05/science/cosmic-census-finds-billions-of-planets-that-could-be-like-earth.html>. Pierce, Rod. Probability Line. 15 December 2016. 12 June 2017. <http://www.mathsisfun.com/probability_line.html>. Robert Moses, Charles Cobb. Radical Equations: Civil Rights from Mississippi to the Algebra Project. Beacon Press, 2001. Scharf, Caleb. Is Earth’s Life Unique in the Universe? . 15 July 2014. 10 4 2017. The School District of Philadelphia. School Profile: Academy at Palumbo. 1 October 2016. 14 June 2017. <https://webapps1.philasd.org/school_profile/view/2620>.
PA Common Core Math Standards Speaking and Listening: Standards of Mathematical Practice: