Author: Shuang-Ching Su
School/Organization:
West Philadelphia High School
Year: 2006
Seminar: Probability and Statistics in the Social Sciences
School Subject(s): Math
Which of the following equations are valid forms of the Binomial Theorem?
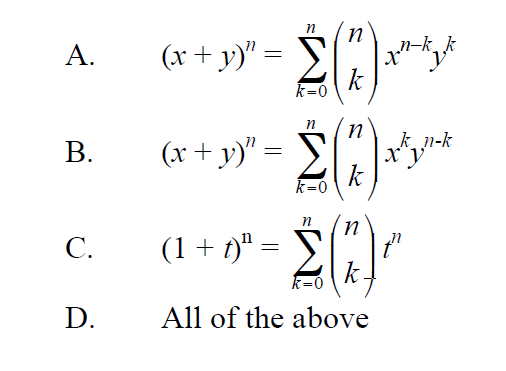
If you choose D as the answer, congratulations! Please prove your answer then. As high school mathematics teachers, we certainly hope our students are able to handle a challenging question like this.
This article presents a curriculum unit pertaining to Pascal’s triangle and the Binomial Theorem. It is intended to serve as a reference framework for high school seniors who seek to conduct a senior project in mathematics.
The curriculum unit is based on lesson plans and class activities in my Discrete Mathematics classes in a period of approximately two weeks. In each lesson during this period, we proved one or two properties of Pascal’s triangle or the Binomial Theorem. At the end of the curriculum unit, students put together their worksheets on a construction paper as a project.
Download Unit: 06.03.03.pdf
Did you try this unit in your classroom? Give us your feedback here.
All seniors at WPHS are required to complete a senior project in order to graduate. According to my survey, no senior projects in my classes were mathematics oriented. Most of the senior project topics were assigned to them, at least in the Business Education and Technology Academy at WPHS, as I was told. Is it feasible for an average high school senior to handle a mathematics-based senior project? To undertake a senior project in mathematics, the student must show interest in mathematics or at least feel confident in his or her mathematical skills. When access to previous senior projects or help in mathematics is not available locally, students tend to avoid any mathematical project topics. This unfortunate situation prompted me to design this curriculum unit to show students the feasibility of conducting senior projects in mathematics if they choose to. Another incentive of mine is to demonstrate a proof of non-trivial nature to students. Proofs are an essential part of mathematics; they are the primary vehicles used to convey mathematical thinking and sharpen students’ problem solving skills. Unfortunately, proofs did not receive the treatment they deserve in high school mathematical curricula (PF-1). Because a successful curriculum in mathematics must focus on 1) definitions and precisions, and 2) abstracting reasoning (CU-1), a senior project based on this curriculum unit poses a challenge for low-achieving students. A challenging project, however, will benefit all seniors whether they are bound for college or the workforce (RB-1). The curriculum unit is part of the Discrete Mathematics. It bridges the gap between Chapter 11 – Series and Patterns of the Algebra 2 textbook (TB-1) and Chapter 12.5 – Binomial Distributions. The curriculum unit aims to help high school seniors practice fundamental mathematical skills, including mathematical induction, proofs of some properties of Pascal’s triangle, and proofs of the Binomial Theorem and some of its applications, including one to binomial probability. By completing worksheets in classes, students begin with constructing Pascal’s triangle in numbers and then in combination symbols. Students learn to calculate number sequences with graphic calculators, such as TI-83/84 Plus. Students then identify and derive Pascal’s rule that underlines the construction of Pascal’s triangle. With the knowledge of Pascal’s rule, students proceed to observe how the Binomial Theorem can be proved by mathematical induction. Students also prove some interesting number patterns embedded in Pascal’s triangle with the Binomial Theorem. Finally, an alternative form of the Binomial Theorem is derived and its application shows the connection of the Binomial Theorem to binomial probability. For details, please refer to the Curriculum Unit Flowchart in the Resources section. The curriculum unit supports NCTM standard that expects high school students to recognize reasoning and proofs as fundamental aspects of mathematics (ST-1). It also supports the Philadelphia Standards: Patterns, Algebra, and Functions – Grades 12-9 (ST- 2).Objectives
The curriculum unit employs worksheets, and group activities to help students pick up inductive and deductive reasoning skills. The worksheets implement scaffolding by including clear definitions, step-by-step instructions, numerical examples, formula explanations, and hints to help students comprehend abstract symbol operations. There is also a worksheet, and transparency on the format and an example of the seq() function available on the TI-83/84 graphic calculator. The curriculum unit was taught in a two-week period during which students compete worksheets through group activities. Each group can be up to four students with one student designated as the group leader. In the class, score discussion, TGT (Teams, Games, Tournaments), think-pair-share, or other teaching strategies (SG-1) (SG-2) may be employed to assist students in reaching the standard. Homework assignments for the curriculum unit are adopted from the textbook (TB-1). The assignment includes Internet search, proofs, and a mini project. The curriculum unit concludes with a test to assess the effectiveness of the curriculum unit. Refer to the Resources section for a list of specific assignments and teacher resources for the curriculum unit.
Subject: 11.7 Pascal Triangle Measurable objectives: Warm-Up: Show that &5# = & 4# + & 4# . $ 3! $ 2! $ 3! Class work: % ² % ² % ² Refer to page 735 of the textbook. Study the first six rows of Pascal’s triangle. Encourage students to make observations on how the numbers are constructed, as shown below. Observations: The kth element in the nth row of the Pascal triangle equals the binomial coefficient & n # where we start counting row number from 0. k % ² 1 = & 3# , 3 = & 3# , 4 = & 4# , etc. $ 0! $1 ! $1 ! % ² % ² % ² Pascal’s triangle construction starts from the top. In every row, the first and the last numbers equal 1. A generic entry of Pascal’s triangle is obtained by summing up the two entries just above it. For example, & 4# = & 3# + & 3# . Convince yourself that &5# = & 4# + & 4# . $1 ! $ 0! $1 ! $ 3! $ 2! $ 3! % ² % ² % ² % ² % ² % ² In general, & n + 1# = & n # + & n # . (Pascal’s rule) $ k ! $ k ¢ ! $ ! % ² % 1² % k ² Prove nCr + nCr+1 = n+1Cr+1 is true for all integers r and n, where 0 ≤ r ≤ n. Group activity: k nCk with % ² & n # . The equation becomes& n # + & n # = & n + 1# . $ k ! $ k ¢ ! $ ! $ ! % ² % 1² % k ² % k ² k & n # $ k ! % ² n! k!(n ! k )! % ² Lesson 1. $ ! $ ! $ ! % 1² % ² % ² Materials: Pages 794 ~ 798, Schultz, Ellis, Hollowell, Kennedy, Engelbrecht, (2004), Algebra 2, Holt Rinehart, and Winston, ISBN: 0-03-070044-2 Handout: A Proof of Pascal’s rule Daily homework: Construct a 6-row Pascal’s triangle in combination notation. Handout: Lesson 1 – A Proof of Pascal’s rule Given that & n # = n! , show that & n # + & n # = & n + 1# , where 0 k ≤ n. $ k ! k!(n ! k )! $ ! % 1² $ ! $ ! % k ² % k ² Directions: Complete the worksheet as a group activiy. Read the Pascal’s rule section to complete the proof table of Pascal’s rule. Pascal’s rule Pascal’s rule states that the number of ways of choosing k objects out of n + 1 objects is equal to the number of ways of choosing k – 1 objects out of n objects plus the number of ways of choosing k objects out of n objects. Let’s consider an example of choosing 3 apples out of 8 apples (PR-1). How many ways are there? It is &8# . Suppose there is a golden apple among the 8 apples. The Remaining 7 apples are red. No matter how you choose the apples, there are only two situations. Either the golden apple is among the 3 apples you choose or it is not among the 3 apples of your choice. Case 1: If the golden apple is among your choice, you need to choose only 2 additional (red) apples from the remaining 7 red apples. For this case, the number of ways you can choose is & 7# . 2 Case 2: If the golden apple is not among your choice, you must choose 3 apples from the remaining 7 red apples. For this case, the number of ways you can choose is & 7# . 3 % ² Thus, &8# = & 7# + & 7# . $ 3! $ 2! $ 3! % ² % ² % ² Proof: $ k ¢ ! $ k ! % 1² % ² $ ! $ ! % 2² % 3² 2 k!(n + 1 ! k )! 3!(5!) k!(n + 1 ! k )! 3!(8 ! 3)! $ k ! % ² $ 3! % ² Subject: 11.8 Binomial Theorem Measurable objectives: Warm-Up: Expand (x – 2)3. Class work: Expand (a – b)3. Score discussion: Have students carry out (a – b)3 polynomial multiplication in vertical format. Then have them substitute a by x, b by 2 to find the answer to the warm-up activity. Page 742, Copy Binomial Theorem to your notebook. (x + y)n = n ¢ n $ xn–kyk !% k ² k =0 & # Group Activity: prove the Binomial Theorem; refer to the handout: Lesson 2. Materials: Pages 741 ~ 744, Schultz, Ellis, Hollowell, Kennedy, Engelbrecht,, (2004), Algebra 2, Holt Rinehart, and Winston, ISBN: 0-03-070044-2 TI-83 Plus graphic calculators Handout: A Proof of the Binominal Theorem Slide: TI-83/84 Plus seq() Function Format Daily homework: [Page 745 of the textbook, #22] Write the summation as a binomial raised to a power; then write it in expanded form: 6 ¢6 $ x6–kyk !% k ² k =0 & # Handout: Lesson 2 – A Proof of the Binomial Theorem Directions: Complete the worksheet as a group activity. Your mission is to fill out the missing reasons by following the instructions in {Hint: …} in Steps 1, 2, 3, 4, and 9 forn the proof of the Binomial Theorem – version 1. For version 2, fill in the blanks in the Reason column. We will prove that version 2 is equivalent to version 1. Here is the Binomial Theorem:(x + y)n = n ¢ n $ xn–kyk … Form 1 !% k ² k =0 & # (x + y)n = n ¢ n $ xkyn-k… Form 2 !% k ² n # = k =0 & n! # are the binomial coefficients, and n! denotes the factorial of n; that is, $ k ! k!(n ! k )! % ² n! = n(n – 1)(n – 2)…(2)(1). Mathematical Induction The mathematical induction consists of two steps: The proposition following the word “if” in the inductive step is called the induction hypothesis (or inductive hypothesis). To perform the induction step, we assume the induction hypothesis (that the statement is true for n = m) and then uses this assumption to prove the statement for n = m + 1. The idea behind mathematical induction is like a donimo effect. In order to prove that a statement about natural numbers is true for all natural numbers, we first verify that the statement is true for the number 1. Then we prove that if it is true for a natural number m, it must be true for m + 1. Since it is indeed true for the number 1, it must be true for the number 2. Since it is true for the number 2, it must be true for the number 3, and so on. The following sketch illustrates this idea. Number line The Binomial Theorem (x + y)n = n ¢ n $ xn–kyk … Form 1 !% k ² k =0 & # Proof (BT-1): When n = 1, (x + y)1 = ¢1 $ x1–kyk = &1 # x1–0y0 + &1# x1–1y1 = &1 # x + &1# y = x + y. !% k ² $ 0! $ ! $ 0! $ ! k =0 & # % ² %1² % ² %1² Assume (x + y)m = m ¢ m $ xm–kyk, which is the induction hypothesis. We want to show !% k ² k =0 & # that (x + y)m+1 = m+1 ¢ m + 1$ xm+1–kyk. !% ² k =0 & # For n = m + 1, m m !% k ² !% k ² k =0 & # k =0 & # m m !% k ² !% k ² k =0 & # k =0 & # !% k ² y + !% k ² x y k =1 & # k =0 & # m m+1 !% k ² !% k ( ² k =1 & # k =1 & 1# !% k ² y + !% k ( ² x y + y k =1 & # k =1 & 1# + 1) = xm+1 + ([$ k ! + $ k ¢ !] xm+1–kyk + ym+1 k =1 % ² % 1² = xm+1 + !% k ² xm+1–kyk + ym+1 k =1 & # & m # + & m # = & m + 1# ?} $ k ! $ k ¢ ! $ k ! % ² % 1² % ² = !% k ² xm+1–kyk + ym+1 k =0 & # = !% k ² xm+1–kyk k =0 & # The Binomial Theorem (x + y)n = ¢ n $ xkyn-k… Form 2 n !% k ² k =0 & # Proof-1: n !% k ² k =0 & # $ 0 ! $1 ! $ 2 ! $ n ¢ ! $ n ! % ² % ² % ² % 1² % ² $ n ! $ n ¢ ! $ n ¢ 2! $1 ! $ 0 ! % ² % 1² % ² % ² % ² n !% n ( k ² k =0 & # n !% k ² k =0 & # Proof-2: !% k ² k =0 & # !% k ² k =0 & # !% k ² k =0 & # !% k ² k =0 & # Subject: 11.8 Binomial Theorem Measurable objectives: Warm-Up: Given that & n # = n! , show that & n # = & n # , where 0 ≤ k ≤ n. $ k ! k!(n ! k )! $ k ! $ n ¢ k ! % ² % ² % ² Class work: n ¢ n $ = 2n, by using the Binomial Theorem. !% k ² k =0 & # Proof: We want to show that 2n = n ¢ n $ …(1) !% k ² k =0 & # (x + y)n = ¢ n $ xn–kyk …(2) n !% k ² k =0 & # Compare Equations (1) and (2). What values of x and y will make (x + y)n = 2n? If x = y = 1, what is xn–k? What is yk? n !(% k ² k =0 & # Ask students to calculate 11n where n = 0 through to 6. 110 = 1 111 = 11 112 = 121 113 = 1,331 114 = 14,641 115 = 160,151 116 = 1,771,561 Encourage students to compare powers of 11 and the top 7 rows of Pascal’s triangle, shown above. What conclusion can we make? Ask students why row 6 and row 7 do “not” seem to match 160,151 and 1,771,561, respectively. Solicit students to explain why they do match. We want to show that ¢ n $ 10n–k ) = (11)n….(3) n !(% k ² k =0 & # n ¢ n $ xn–kyk = (x + y)n …(4) !% k ² k =0 & # Compare Equations (3) and (4). What values of x and y will help us to achieve the objective? Encourage students to suggest their answers. If x = 10, y = 1, what is yk? n & n # 10n–k, what is 10n–k? [Place value] k % ² Materials: Pages 753 ~ 755, Schultz, Ellis, Hollowell, Kennedy, Engelbrecht,, (2004), Algebra 2, Holt Rinehart, and Winston, ISBN: 0-03-070044-2 Handout: An Application of the Binomial Theorem and Binomial Probability Daily homework: [Page 746 of the textbook, #56] The value &10#n apppears as a $ ! % ² coefficient of two different terms in the expansion of (a + b)10. What are the two terms? Handout: Lesson 3 – An Application of the Binomial Theorem and Binomial Probability Directions: Solve the following problem by using the Binomial Theorem and binomial probability. Fill in the blanks in the Reason column. n The Binomial Theorem: (x + y)n = ¢ n $ xkyn-k !% k ² k =0 & # Binomial probability: P = & n # pk(1 – p)n-k k % ² Problem: The probability that a driver is not wearing a seat belt is 0.18. Find the probability that at least 2 of 10 drivers are not wearing seat belts. Hint: Refer to Example 2 on page 803 of the textbook. Procedure: Statement n !% k ² k =0 & # n !% k ² k =0 & # binomial probability.) 10 !% k ² k =0 & # 1 10 !% k ² !% k ² k =0 & # k =2 & # !% ² pk(1 – p)10–k = 1 – !% ² pk(1 – p)10–k k =2 & k # k =0 & k # $ 0 ! $1 ! % ² % ² $ 0 ! $1 ! % ² % ² (10)(0.18)(0.82)9 ≈ 0.302Lesson Plan – 1
Row
0:
1
Row
1:
1
1
Row
2:
1
2
1
Row
3:
1
3
3
1
Row
4:
1
4
6
4
1
Row
5:
1
5
10
10
5
1
$ !
$ !
$ !
=
k ¢ k k
% ²
k ¢
$ !
$ !
$ !
Statement
Numerical Example
Reason
& n # + & n #
& 7# + & 7#
n = 7, k = 3, k –1 =
=
n!
+
7! + 7!
1.
(k ! 1)!(n ! (k ! 1))!
2!(7 ! 2)! 3!(7 ! 3)!
n!
k!(n ! k )!
=
k(n!)
+
= 3(7!) + 5(7!)
2. n +1 – k = 5
k(k ! 1)!(n + 1 ! k )!
3(2!)(7 ! 2)! 3!(5)(7 ! 3)!
(n + 1 ! k )(n!)
k!(n + 1 ! k )(n ! k )!
=
k(n!)
+ (n + 1 ! k )(n!)
= 3(7!) + 5(7!)
3.
k!(n + 1 ! k )!
k!(n + 1 ! k )!
3!(5!) 3!(5!)
= k(n!) + (n + 1 ! k )(n!)
= 3(7!) + 5(7!)
4.
k!(n + 1 ! k )!
3!(5!)
= (k + n + 1 ! k )(n!)
= (3 + 5)(7!)
5.
k!(n + 1 ! k )!
3!(5!)
= (n + 1)(n!)
= 8(7!)
6.
= (n + 1)!
= 8!
7.
= & n + 1#
= &8#
8.
Lesson Plan – 2
k
Statement
Reason
(x + y)m +1 = (x + y)(x + y)m
1. {Hint: Textbook page 95}
= x(x + y)m + y(x + y)m
2. {Hint: Textbook page 87}
= x ¢ m $ xm–kyk + y ¢ m $ xm–kyk
3. {Hint: What is the name of the proposition after the word “if” in Mathematical Induction? See above. What is the proposition? See the Induction step.}
= ¢ m $ xm+1–kyk + ¢ m $ xm–kyk+1
4. {Hint: Textbook page 95, and page 87}
= xm+1 + m ¢ m $ xm+1–k k m ¢ m $ m–k k+1
5. Extracting the first term, xm+1, from the first summation (k = 0)
= xm+1 + ¢ m $ xm+1–kyk + ¢ m $ xm+1–kyk
6. Adjusting the index k in the second summation so that it starts with 1 instead of 0
= xm+1 + m ¢ m $ xm+1–k k m ¢ m $ m+1–k k m+1
7. Extracting the last term, ym+1, from the second summation (k = m
m & m # & m #
8. Combining the two summations in the middle
m ¢ m + 1$
9. {Hint: What is the name of the property that
m ¢ m + 1$
10. Merging xm+1 to the summation as the first term (k = 0)
m+1 ¢ m + 1$
11. Merging ym+1 to the summation as the last term (k = m + 1)
Statement
Reason
(x + y)n = ¢ n $ xn–kyk
1.
= & n # xn + & n # xn–1y + & n # xn–2y2 + … + & n # xyn–1 + & n # yn
2.
= & n # yn + & n # xyn–1 + & n # x2yn–2 +… + & n # xn–1y + & n # xn
3.
= ¢ n $ xkyn-k
4.
= ¢ n $ xkyn-k
5.
Statement
Reason
(x + y)n = n ¢ n $ xn–kyk
1.
(y + x)n = n ¢ n $ xn–kyk
2.
(y + x)n = n ¢ n $ ykxn–k
3.
(x + y)n = n ¢ n $ xkyn-k
4.
Lesson Plan – 3
$ !
7
$ !
Reason
(x + y)n = ¢ n $ xkyn-k
1.
(p + (1 – p))n = ¢ n $ pk(1 – p)n–k
2. x = ; y = (This is the connection between the Binomial Theorem and
110 = ¢10$ pk(1 – p)10–k
3. n = ; p + (1 – p) =
1 = ¢10$ pk(1 – p)10–k + ¢10$ pk(1 – p)10–k
4.
10 ¢10$ 1 ¢10$
5. Why? P(E) = 1 – P(EC)
= 1 – ( &10# (0.18)0(0.82)10-0 + &10# (0.18)1(0.82)10-1)
6. p = ; 1 – p =
= 1 – ((0.82)10 + (10)(0.18)(0.82)9)
7. &10# = ; &10# =
≈ 1 – (0.137 + 0.302) = 1 – 0.439 = 0.561
8. (0.82)10 ≈ 0.137
Mathematical induction
[BT-1] http://planetmath.org/?op=getobj&from=objects&id=338 This web link presents a proof of the Binomial Theorem. The 2-column proof of the worksheet is based on this proof. [CU-1] Milgram, James R., Wu, Hung-Hsi, 2006, “The Key Topics in a Successful Math Curriculum,” (http://math.berkeley.edu/~wu/six-topics1.pdf) Department of Mathematics, Stanford University & University of California, Berkeley [IV-1] Dancis, Jerome, January 2, 2006, “Interview with University of Maryland Professor Jerome Danics,” http://www.baltimorecp.org/newsletter/jerome_dancis.pdf, p. [PF-1] http://www.chatham.edu/pti/ProofinMathematics/proof_curriculum.htm [PT-1] http://en.wikipedia.org/wiki/Pascal%27s_rule This web link presents a more general (and abstract) explanation of Pascal’s rule. [PT-2] http://mathforum.org/workshops/usi/pascal/index.html This web link provides many worksheets for Pascal’s triangle. It also has links to NCTM Standards. [RB-1] Barton, Rhonda, Fall 2004, “The Challenge of Reinventing High School,” http://www.nwrel.org/nwedu/10-01/brief/, Research Brief, Northwest Education, Volume 10, Number 1, Northwest Regional Educational Laboratory, p. 42. [ST-1] http://standards.nctm.org/document/chapter7/reas.htm Reasoning and proof standard for grades 9-12 [ST-2] http://www.philsch.k12.pa.us/teachers/frameworks/grid/gridmast.htm This web link allows you to find any subject standards for any grade within the School District of Philadelphia. For the standards included in this curriculum unit, you will use subject: Math, level: Algebra II, standard: 4.Pattern Algebra Functions [SG-1] http://www.aea267.k12.ia.us/framework/index.php?page=framework-teaching [SG-2] http://www.education.tas.gov.au/english/strategy.htm These web links contain a handy matrix of teaching strategies with strategy descriptions in PDF or HTML format. [TB-1] Schultz, Ellis, Hollowell, Kennedy, Engelbrecht, (2004), Algebra 2, Holt Rinehart, and Winston, ISBN: 0-03-070044-2. It is the Algebra 2 textbook used in the School District of Philadelphia (SDP). Homework assignments All assignments are due the following school day unless specified otherwise. $ 4! $ 3! $ 4! % ² % ² % ² expanded form: !¢6 $ x6–kyk. 6 % k ² k =0 & # 3 2 $ 7 ! % ² expansion of (a + b)10. What are the two terms? TI-83/84 Plus seq() Function Format seq(expression, variable, begin, end [, increment]) Arguments Expression = 7 nCr X Variable = X Begin = 0 (Initial value of the variable) End = 7 (Final value of the variable) Increment = 1 (default value, optional) Example for Row 7 of Pascal Triangle Input: 2ND LIST OPS 5:seq( Display: seq( Input: 7 MATH PRB 3:nCr Display: seq(7 nCr Input: [X,T,θ,n] , [X,T,θ,n] , 0 , 7 , 1 ) Display: seq(7 nCr X, X, 0, 7, 1) {1 7 21 35 35 2… Row 7 of Pascal’s triangle: {1 7 21 35 35 21 7 1} Name: Period: Date: Discrete Mathematics, Chapter 11.7 ~ 11.8 Test, 2005-2006 Q-1. Using the form below, construct an 8-row Pascal’s triangle in combination notation. (10%) [Hint: Refer to the textbook, page 736.] Q-2. Given the summation expression 6 ¢6 $ x6–kyk, !% k ² k =0 & # Q-3. Given& n # = k n! k!(n ! k )! where n! denotes the factorial of n; that is, n! = n(n – 1)(n – % ² 2)…(2)(1). Prove that& n # = & n # , where 0 ≤ k ≤ n. (10%) $ k ! $ n ¢ k ! % ² % ² Q-4. (a) Use multiplication (in vertical format) and the distributive property to expand (x – 2y)3 as a polynomial with decreasing powers of x. Show your work. (10%) (b) Use the Binomial Theorem to expand (x – 2y)3 as a polynomial with decreasing powers of x. Show your work. (10%) [Hint: Refer to Q-5.] Q-5. The Binomial Theorem states that (x + y)n = n ¢ n $ xn–kyk, where & n # = !% k ² $ k ! k =0 & # % ² n! k!(n ! k )! are the binomial coefficients, and n! denotes the factorial of n; that is, n! = n(n – 1)(n – 2)…(2)(1). n !% k ² k =0 & # (b) Prove that ¢ n $ 10n–k) = (11)n. (10%) n !(% k ² k =0 & # Q-6. (a) How are the Fibonacci numbers constructed? [Hint: Refer to the textbook, page 693.] (10%) Standards: [ST-1] http://standards.nctm.org/document/chapter7/reas.htm [ST-2] Philadelphia Standards: Patterns, Algebra, and Functions – Grades 12-9 Name: Period: Date: Project: Pascal’s Triangle and the Binomial Theorem Introduction The objective of this project is to help you practice inductive and deductive reasoning by recognizing and proving some patterns of Pascal’s triangle and the Binomial Theorem. Procedure k % ² Use the supplied worksheet. n ¢ n $ = 2n, by using the Binomial Theorem. Attach the proof to the poster or !% k ² k =0 & # construction paper. n !(% k ² k =0 & #paper. (Hint: Refer to #28 on page 739 of the textbook.) Grading scheme The project is worth 100 points that translate to 15 extra points of for the 3rd marking period report card. Your score will be based on how many correct steps are included in your project. Each step is worth 10 points. Your score for each step will be proportional to the number of correct answers if more than one answers are expected for the step.
Date
Assignment
March 17, 2006
Use Google to search more information on Pascal’s Triangle. Write one page summary report on Pascal’s triangle.
March 20, 2006
Show that &5 # = & 4# + & 4# .
March 21, 2006
Construct a 6-row Pascal’s triangle in combination notation.
March 23, 2006
Create a tree diagram or table to illustrate all possible outcomes for 3 coin tosses. For example, tossing a “head, head, tail” is represented by “H-H-T”.
March 24, 2006
Use multiplication and the distributive property to expand (x + y)4 as a polynomial with decreasing powers of x.
March 27, 2006
Use multiplication and the distributive property to expand (x + y)5 as a polynomial with decreasing powers of x.
March 28, 2006
Expand (2x – y)3.
March 29, 2006
Write the summation as a binomial raised to a power; then write it in
March 30, 2006
Expand ( 2 x + 1 y)4.
March 31, 2006
The value &10# appears as a coefficient of two different terms in the
April 3, 2006
(Extra credits) Mini Project: Let a + bi = (1 + i)11, where a, b are real numbers, and i = ! 1 . Find a, and b by using the Binomial Theorem. (Hint: Refer to page 316 of the textbook: Imaginary Numbers, Complex Numbers.)
$ !
Appendix
$ !
Standards: [ST-1] http://standards.nctm.org/document/chapter7/reas.htm [ST-2] Philadelphia Standards: Patterns, Algebra, and Functions – Grades 12-9 Name: Period: Date: Project: Pascal’s Triangle and the Binomial Theorem Introduction The objective of this project is to help you practice inductive and deductive reasoning by recognizing and proving some ptterns of Pascal’s triangle and the Binomial Theorem. Procedure k % ² Use the supplied worksheet. n ¢ n $ = 2n, by using the Binomial Theorem. Attach the proof to the poster or!% k ² k =0 & # construction paper. !(% k ² k =0 & # paper. (Hint: Refer to #28 on page 739 of the textbook.) Grading scheme The project is worth 100 points that translate to 15 extra points of for the 3rd marking period report card. Your score will be based on how many correct steps are included in your project. Each step is worth 10 points. Your score for each step will be proportional to the number of correct answers if more than one answers are expected for the step. SEE PDF FOR PHOTOS.Appendix
$ !